onde
(latin unda)

Modification de l'état physique d'un milieu matériel ou immatériel, qui se propage à la suite d'une action locale avec une vitesse finie, déterminée par les caractéristiques des milieux traversés.
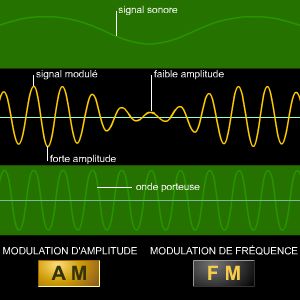

Les techniques de télécommunication – radio, télévision, téléphone – nous ont rendu familière la présence des ondes. Avant de donner lieu à des utilisations de cette importance, les phénomènes ondulatoires ont progressivement occupé une place de plus en plus grande en physique. Ils ont révélé leur présence dans les domaines les plus divers, au point d'apparaître comme intimement liés, d'une certaine façon, à la constitution de la nature en ses aspects fondamentaux. Si l'onde sonore s'explique en termes mécanistes par les mouvements des particules dont l'air est constitué, il n'y a rien de tel, par exemple, pour les ondes hertziennes. Leur analyse mathématique n'en revêt que plus d'importance. Avec la mécanique ondulatoire, on est même tenté de dire qu'il ne s'agit plus que de mathématiques.
1. Les différents types d’ondes
1.1. Les ondes mécaniques progressives
1.1.1. Les vagues
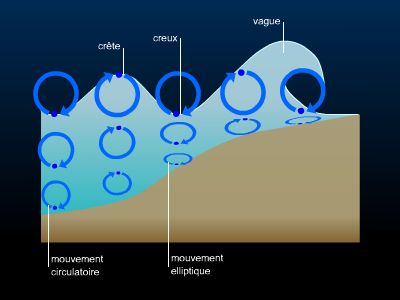
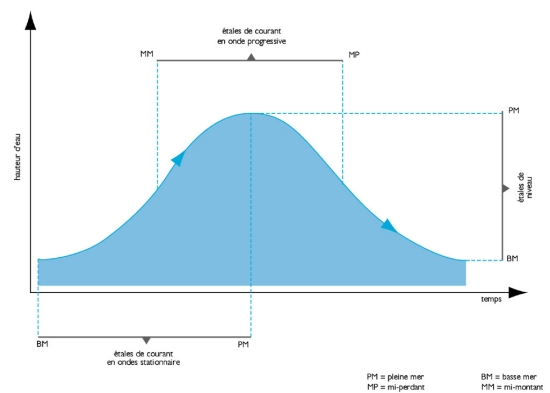
Un objet – une simple goutte – qui tombe sur la surface d'une eau calme y produit des ondulations. Ce train d'ondes est constitué de quelques cercles qui, issus de la source du phénomène, vont en s'agrandissant et qui finissent par s'affaiblir. Si un corps flotte immobile, les ondes, en l'atteignant, ne le déplacent pas à la surface de l'eau dans le sens de leur mouvement. Elles l'agitent verticalement, tout comme le feraient les vagues de la mer. « Onde » vient d'ailleurs de unda, qui désigne l'eau de la mer, avec les mouvements qui s'y peuvent voir. Les rides circulaires à la surface de l’eau se propageant dans deux directions sont qualifiées d’ondes mécaniques progressives à deux dimensions.
1.1.2. Les cordes
Une autre manière de produire un phénomène semblable consiste à déployer une corde, sans nécessairement attacher l'une de ses extrémités, et à secouer l'autre assez vigoureusement. Chaque secousse engendre une déformation que l'on voit se propager le long de la corde. En faisant se succéder les secousses, on obtient un train d'ondes. Ces ondes se propageant dans une seule direction sont qualifiées d’ondes mécaniques progressives à une dimension.
1.1.3. Les ondes sonores ou acoustiques

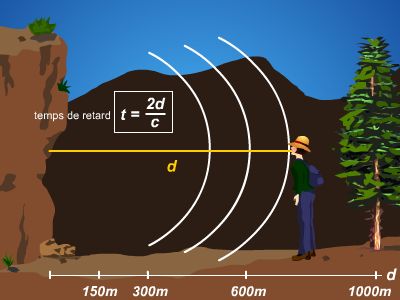
C'est un phénomène analogue qui a servi à expliquer la nature physique du son et à étudier en finesse ses propriétés. La corde de lyre que l'on pince vibre rapidement. Ses vibrations se transmettent à l'air, s'éloignant dans toutes les directions. Les ondes acoustiques se propageant dans trois directions sont qualifiées d’ondes mécaniques progressives à trois dimensions. Une oreille, placée n'importe où autour, reçoit des ondes (→ audition). Les vibrations sont communiquées par l'air au tympan. La source peut être n'importe quelle membrane susceptible de vibrer : la peau d'un tambour, mais aussi les cordes vocales.

En vibrant, la membrane pousse l'air tout proche ; les particules d'air déplacées poussent à leur tour leurs voisines et ainsi de suite. Si l'on pouvait voir un petit corps flotter dans cet air, on observerait toutefois que l'agitation très rapide qu'il subit sur place ne se fait pas comme celle d'un bouchon sur l'eau. Ce dernier oscille verticalement, tandis que les ondes s'éloignent horizontalement de leur source : de telles ondes sont dites transversales. Dans le cas de l'air, l'objet est agité dans la direction même du mouvement des ondes : celles-ci sont dites longitudinales.
1.2. Les ondes mécaniques stationnaires
Les ondes des trois genres mentionnés auparavant peuvent donner lieu à des phénomènes stationnaires. Si un caillou tombe dans l'eau d'un bassin, les ondes se réfléchissent sur le bord. De même, si l'on secoue sans cesse le bout d'une corde qui est fixée à l'autre extrémité et légèrement tendue, les ondes repartent de cette extrémité. Certains points de la corde peuvent ne pas bouger du tout, alors que tout s'agite autour d'eux, parce que le mouvement qui y est créé par les ondes allant dans un sens est constamment contrarié par celui qu'y induisent les ondes allant dans l'autre sens. Les points pour lesquels l'oscillation est maximale sont appelés les ventres ; ceux pour lesquels elle est nulle, les nœuds.
Semblablement, si deux pointes vibrent ensemble à la surface d'un liquide, les deux trains d'ondes ainsi entretenus laissent immobiles des points de cette surface formant des lignes entières, des hyperboles très précisément. C'est le phénomène des interférences, difficile à observer sans un éclairage adapté.
1.3. La lumière et les ondes électromagnétiques
1.3.1. La nature ondulatoire de la lumière

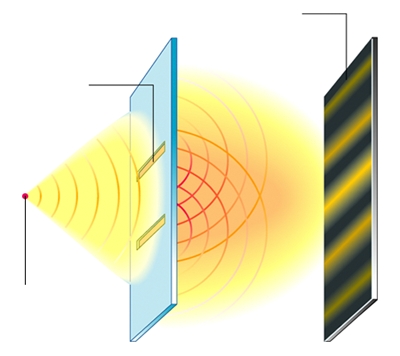
Thomas Young (1773-1829) montra que des interférences peuvent s'observer aussi en optique : une lumière monochromatique passant par deux fentes parallèles donne sur un écran une alternance de franges brillantes et de franges sombres. L'apparition de ces dernières ne s'expliquerait pas si la lumière était constituée de corpuscules en mouvement, comme Isaac Newton (1642-1727) en avait fait admettre l'idée.
Augustin Fresnel (1788-1827) montra que, au contraire, si la lumière est de nature ondulatoire, les interférences s'expliquent jusque dans leurs aspects quantitatifs. Ainsi s'installa l'idée que l'espace est rempli par un milieu imperceptible, l'éther, dont les vibrations constituent la lumière, tout comme les vibrations de l'air et d'autres milieux matériels constituent le son. La découverte du phénomène de polarisation par Étienne Malus (1775-1812) contraria rapidement l'idée qu'il s'agissait, comme dans le cas du son, d'ondes longitudinales.
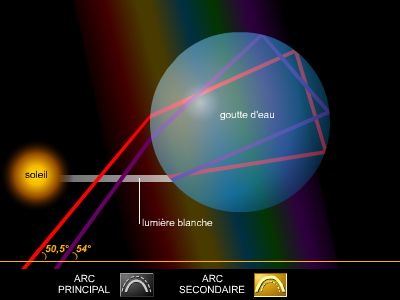
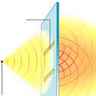
Un autre phénomène bien connu, la diffraction, s'explique mieux dans une théorie ondulatoire que dans une théorie corpusculaire de la lumière. On l'obtient en faisant passer de la lumière par un trou que l'on rétrécit. Le pinceau de lumière commence par s'affiner mais, à partir d'une certaine petitesse du trou, au lieu de continuer de se rétrécir, le pinceau se disperse.
1.3.2. Les ondes électromagnétiques

Un demi-siècle plus tard, James Maxwell (1831-1879) ayant réduit l'électricité et le magnétisme à quelques formules, il apparut par le calcul que la propagation des actions électromagnétiques devait prendre la forme d'ondes. Heinrich Hertz (1857-1894) les produisit et les étudia expérimentalement. Transversales elles aussi, elles se déplacent à une vitesse qui se trouve être celle de la lumière. Ainsi s'achemina-t-on vers la conclusion que la lumière n'est elle-même qu'une onde électromagnétique, occupant une modeste place dans la gamme des cas possibles. Si l'on préfère, ces ondes constituent une lumière généralement invisible, c'est-à-dire insensible à l'œil, à l'exception d'une petite partie. L'éther que l'on cherchait à mieux connaître n'était plus le siège des seules ondes lumineuses, mais celui des ondes électromagnétiques en général. Les diverses propriétés qu'il se devait de posséder étaient si difficiles à accorder entre elles qu'il constituait une grande énigme. On a fini par renoncer à cette notion.
On accepte l'idée qu'il puisse y avoir de telles ondes sans qu'elles soient les ondulations d'un milieu. On sait seulement que ce sont des charges électriques en mouvement qui les produisent.
1.3.3. La dualité onde-corpuscule

Albert Einstein (1879-1955), l'année même où il proposa la théorie de la relativité restreinte (1905), donna une explication de l'effet photoélectrique. Elle consistait à revenir à la conception corpusculaire de la lumière, sans renoncer pour autant à son aspect ondulatoire. Plus généralement, l'onde électromagnétique s'est vu associer un flux de photons, association purement mathématique et qui rendait encore plus intenable l'hypothèse d'un éther. Louis de Broglie (1892-1987), en l'inversant, étendit l'idée à toutes les particules : à chacune on associe une onde. L'expérience a confirmé la justesse de cette hypothèse : il fut établi qu'un faisceau d'électrons est susceptible de donner lieu au phénomène de diffraction.
La mécanique quantique prend désormais pour objets des quantons, qui se comportent comme des corpuscules dans certains contextes expérimentaux et comme des ondes dans d'autres. La fonction d'onde de la particule, obtenue par la résolution de l'équation de Schrödinger, sert à calculer les caractéristiques de son mouvement, mais en termes de probabilité seulement. On ne peut pas annoncer qu'à tel instant la particule sera en tel point, comme on le fait en mécanique classique. On peut seulement calculer avec quelle probabilité elle se trouvera dans telle portion d'espace.
2. Caractéristiques physico-mathématiques des ondes
2.1. Généralités
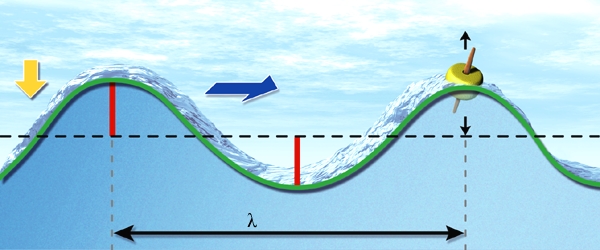
Un mécanisme de production et de propagation des ondes peut être détaillé dans le cas de la surface d'un liquide ou dans celui du son, parce que l'on peut analyser le comportement d'un milieu – le liquide, l'air – en termes mécanistes. Il n'en va plus de même pour les ondes électromagnétiques, et encore moins pour celles de la mécanique ondulatoire, puisqu'il n'y a plus de milieu connu dans ces cas-ci. Une étude générale des ondes doit donc se rabattre sur la description mathématique de la propagation.
→ mécanique.
Il convient de remarquer que, lorsqu'une description mécaniste est possible, elle n'explique pas la toute première apparence. Une onde, qu'il s'agisse d'une vague ou de la déformation d'une corde, se présente spontanément comme quelque chose qui se déplace. C'est ce déplacement qui est désigné par le terme « propagation ». Il ne se présente pas comme le déplacement d'un objet (navire avançant sur l'eau ou anneau coulissant sur une corde). Le phénomène offre le spectacle de quelque chose qui se meut et ne se meut pas à la fois.
Le mécanisme de la production de la perturbation à la source, et de sa transmission par le milieu, explique qu'un corps flottant ainsi que l'eau qui l'entoure montent et descendent alternativement. Il n'explique pas complètement l'illusion que constitue le déplacement de la vague. On peut dire néanmoins que c'est le déplacement transversal de l'eau qui se décale dans la direction de propagation.
2.2. Grandeurs caractéristiques
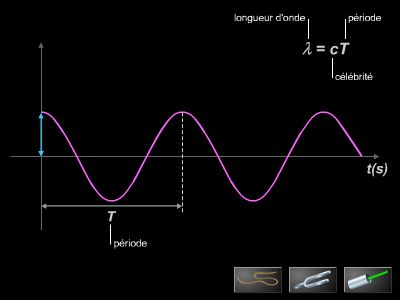
Lorsqu'aucun milieu n'est le siège de la propagation, on peut néanmoins concevoir qu'il y ait, attachée à chaque point de l'espace, une certaine grandeur qui soit l'analogue de l'altitude de la surface de l'eau. En prenant pour niveau de référence celui de la surface liquide au repos par exemple, le phénomène de l'ondulation peut être décrit mathématiquement en donnant, pour chacun des points de la surface, son altitude en fonction du temps. Pour une onde d'une autre nature, le rôle joué précédemment par l'altitude peut l'être par la valeur d'un champ, électrique ou magnétique.
De façon plus générale, en se plaçant en un point P de l'espace, a (t) désignera la valeur, à l'instant t, de la grandeur qui varie.
2.2.1. Période et fréquence
On se place dans l'hypothèse d'une onde entretenue et périodique : en P, la grandeur oscille sans cesse et elle reprend toujours la même valeur au bout d'un même temps T, appelé la période de l'onde. Autrement dit, quel que soit l'instant t,
a (t + T) = a (t)
On appelle alors fréquence de l'onde le nombre d'oscillations complètes que P effectue pendant une unité de temps. La fréquence f (aussi notée N, ou encore ν) est reliée à la période par
f = 1 / T
Si l'on adopte la seconde comme unité de temps, la fréquence s'exprime en hertz, de symbole Hz (ou cycles par seconde).
2.2.2. Longueur d'onde
La longueur d'onde λ est la distance parcourue par l'onde pendant le temps T. Si V est la vitesse de propagation, supposée constante, on a
λ = VT
soit encore
λ = V / f
C'est ainsi que, dans un cas comme celui de la lumière, où la vitesse de propagation est connue (près de 300 000 km.s−1 dans le vide), la détermination expérimentale d'une longueur d'onde permet de trouver la fréquence correspondante.
2.3. Les ondes sinusoïdales

Une situation particulière de grande importance est celle des ondes sinusoïdales, pour lesquelles
a (t) = A (sin ω t + ϕ)
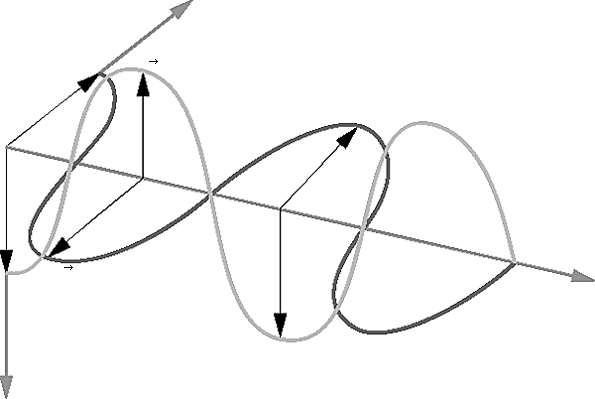
L'importance des ondes sinusoïdales tient à ce qu'elles fournissent un modèle mathématique satisfaisant pour nombre de phénomènes. C'est le cas pour les ondes électromagnétiques en particulier, où se rencontre une complication par rapport aux situations envisagées jusqu'à présent : il n'y a pas, en un point, une grandeur a qui varie sinusoïdalement, mais deux, le champ électrique et le champ magnétique, vecteurs orthogonaux entre eux ainsi qu'à la direction de propagation (le rayon lumineux).
Une autre raison de l'intérêt porté aux ondes sinusoïdales est que l'on sait, depuis les travaux mathématiques de Joseph Fourier (1768-1830), que pour toute fonction périodique, on peut envisager une décomposition sous la forme d'une somme de fonctions sinusoïdales. La connaissance de ces dernières fournit donc la clef de l'analyse d'un phénomène périodique quelconque.
Lorsque t varie, a (t) varie perpétuellement entre − A et A.
• Amplitude. La constante positive A est l'amplitude de l'onde au point P.
• Phase. L'expression ω t + ϕ est appelée la phase ; ϕ est la phase à l'origine, c'est-à-dire la valeur de la phase à l'instant 0.
• Pulsation. Le coefficient ω est la pulsation ; il est lié à la période par T = 2 π / ω et à la fréquence par ω = 2πf ; il s'exprime en radians par seconde (rad / s ou rad.s−1).
La valeur de ϕ est propre au point P où l'on se place. Pour un point P′ autre, la phase à l'origine a une valeur ϕ′, alors que ω et A sont les mêmes partout. Mais si l'on prend pour P′ un point situé à une distance de P égale à la longueur d'onde λ, ϕ′ = ϕ + 2π, de sorte que la grandeur a prend à tout instant la même valeur en P et en P′. On dit que ces points vibrent en phase.
2.4. Aspects énergétiques
Le déplacement d'une onde est en un sens une illusion. Le point de vue énergétique permet au physicien de donner une certaine consistance à ce déplacement. À la source S, on fournit une énergie essentiellement cinétique aux parties de la corde qu'on y agite, celle du mouvement transversal. Cette énergie se transmet de proche en proche. Lorsque l'agitation atteint les parties les plus proches de l'extrémité S′, on peut l'utiliser pour mettre un objet en mouvement, ou pour obtenir d'autres sortes d'effets. Au total, il y a eu transfert progressif d'énergie de la source à l'extrémité. La quantité d'énergie qui se propage est, pourrait-on dire, un pseudo-objet qui s'éloigne de la source. Dans une perspective de communication, on préfère dire qu'un signal est émis en S et propagé jusqu'en S′.
Pour ce qui est de la mécanique quantique, la prise en compte de l'énergie est à la base même de l'association entre l'onde et la particule. Si ν et E sont respectivement la fréquence de la première et l'énergie dont la seconde est porteuse,
E = hν
(relation de Planck-Einstein, où h est la constante de Planck).
De manière analogue, si λ et p sont respectivement la longueur d'onde et la quantité de mouvement,
p = h / λ (relation de de Broglie)
3. Le spectre des ondes électromagnétiques
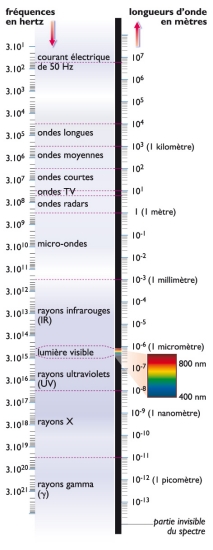
La première application pratique des ondes électromagnétiques a été la télégraphie sans fil, bientôt rebaptisée radiophonie (radiocommunication). La télévision devait suivre. Le radar, quant à lui, n'est rien d'autre que l'utilisation de la propriété qu'ont les ondes électromagnétiques, à l'instar de la lumière, de se réfléchir sur un obstacle. Le fonctionnement s'apparente étroitement à celui de l'écho sonore.
Chacune de ces applications fait appel à un certain domaine des ondes caractérisé par ses longueurs d'onde extrêmes (ou, ce qui revient au même, par ses fréquences-limites). Les cas évoqués ci-dessus sont des exemples d'ondes hertziennes. On désigne ainsi celles dont la longueur d'onde s'étend entre le centimètre et quelques kilomètres. La lumière visible correspond à la bande qui va de 0,4 à 0,8 micromètre. Entre celle-ci et les précédentes se situe le domaine de l'infrarouge. Au-delà, on passe dans l'ultraviolet, puis, entre 3 nanomètres et 0,01 nanomètre, aux rayons X. Enfin viennent les rayons gamma (γ) et le rayonnement cosmique. Les derniers cités, ayant la plus petite longueur d'onde, ont la fréquence la plus élevée. Conformément à la relation E = hν, ce sont leurs photons qui sont porteurs de l'énergie la plus grande. De fait, ultraviolet, rayons X et rayons γ sont connus pour le danger qu'ils représentent pour les organismes vivants, plus grand même pour les derniers que pour les premiers.
Mais c'est aussi par l'analyse de la diffraction qu'un cristal impose aux rayons X que l'on a pu y étudier de manière précise, à partir de 1912, l'arrangement des atomes (cristallographie).
Pour en savoir plus, voir l'article spectre.