géométrique
adjectif
(latin geometricus, du grec geômetrikos)
- 1. Qui relève de la géométrie : Figure géométrique.
- 2. Qui a des formes régulières, des contours nets, simples, rappelant les figures de la géométrie : Décor géométrique.
- 3. Vieux. Qui est exact, précis, mathématique : Avoir une rigueur toute géométrique.
-
Archéologie
4. Se dit du décor des vases produits en Grèce du xie au viiie s. avant J.-C., qui fait une large part aux formes géométriques. - 5. Se dit de la période de l'art grec pendant laquelle se développe ce décor.

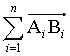 où
où
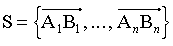 est un système de vecteurs glissants.
est un système de vecteurs glissants.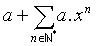 .
.